I don’t do as much Rubik’s cube solving as I used to and I’m afraid I’m going to eventually forget some algorithms. So I decided to write down the ones I use, starting with the PLLs.
The U movements between square brackets at the end indicate the AUF (they are not cube rotations).
Corners only
| Name | Image | Algorithm | Comment |
|---|---|---|---|
| A | 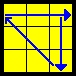 |
x’ R’ D R’ U2 R D’ R’ U2 R2 | |
| A' |  |
x’ R2 U2 R D R’ U2 R D’ R | Inverse of A |
| E | 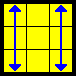 |
(Lw’ U R D’ R’ U’ R D) x’ (Lw’ U’ R D’ R’ U R D) | Actually two OLLs in a row |
Alternatives
| Name | Image | Algorithm | Comment |
|---|---|---|---|
| E | 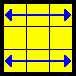 |
z U2 R2 F (R U R’ U’)3 F’ R2 U2 | Longer but very easy to remenber. |
Edges only
| Name | Image | Algorithm | Comment |
|---|---|---|---|
| U | 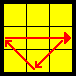 |
R2 U R U R’ U’ R’ U’ R’ U R' | |
| Usym | 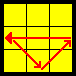 |
L2 U’ L’ U’ L U L U L U’ L | Left-handed U perm |
| H |  |
M2’ U M2’ U2 M2’ U M2' | M2’ with ring finger + middle finger |
| Z | 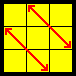 |
M’ U M2’ U M2’ U M’ U2 M2’ [U'] | M2’ with ring finger + middle finger |
Alternatives
| Name | Image | Algorithm | Comment |
|---|---|---|---|
| H |  |
R2 U2’ R U2’ R2’ U2’ R2 U2’ R U2 R2' | Better on bigger cubes |
| Z | 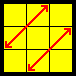 |
R U R’ U R’ U’ R’ U R U’ R’ U’ R2’ U R [U2] | Better on bigger cubes |
Two adjacent corners and two edges
| Name | Image | Algorithm | Comment |
|---|---|---|---|
| T | 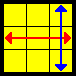 |
(R U R’ U’) R’ F R2 U’ R’ U’ (R U R’ F') | |
| J | 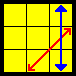 |
(R U R’ F’) (R U R’ U’) R’ F R2 U’ R’ [U'] | Same as T but with the last 4 moves now at the beginning |
| Jsym | 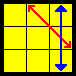 |
L’ R’ U2 R U R’ U2 L U’ R [U] | |
| F | 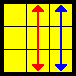 |
R’ U’ F’ (R U R’ U’) R’ F R2 U’ (R’ U’ R U) R’ U R | T perm with an (R’ U’ F’) setup, and a cancellation at the end |
| R | 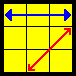 |
(R’ U2 R U2) (R’ F R U R’ U’) (R’ F’ R2) [U'] | |
| Rsym | 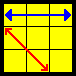 |
(L U2’ L’ U2’) (L F’ L’ U’ L U) (L F L2’) [U] | Left-handed R perm |
The Gs
There is only one algorithm here. The second one is the inverse of the first one (after replacing y’RU’R’ with the equivalent yLU’L). The other two are the left-hand equivalents.
| Name | Image | Algorithm | Comment |
|---|---|---|---|
| G | 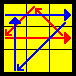 |
(R2 Uw) (R’ U R’ U’ R Uw’) R2’ y (L U’ L') | FU-FUR same, FUL adjacent |
| G' | 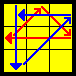 |
y’ (R’ U’ R) y R2’ (Uw R’ U R U’ R) (Uw’ R2') | FU-FUR same, FUL opposite |
| Gsym | 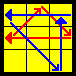 |
(L2’ Uw’) (L U’ L U L’ Uw) L2 y’ (R U’ R') | FU-FUL same, FUR adjacent |
| G’sym | 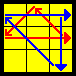 |
y (L U L’) y’ L2’ (Uw’ L U’ L’ U L’) (Uw L2) | FU-FUL same, FUR opposite |
Diagonals
| Name | Image | Algorithm | Comment |
|---|---|---|---|
| V | 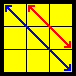 |
(R’ U R’ U’) y (R’ F’ R2 U’) (R’ U R’ F) (R F) | |
| N | 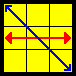 |
(R’ U L’ U2’ R U’ L)2 [U] | |
| Nsym | 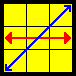 |
(L U’ R U2 L’ U R’)2 [U'] | Left-handed N perm |
| Y | 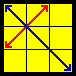 |
F (R U’ R’ U’) (R U R’ F’) (R U R’ U’) (R’ F R F') |
Alternatives
| Name | Image | Algorithm | Comment |
|---|---|---|---|
| V | 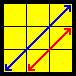 |
z U’ R D (R’ U R U’) z’ (U R’ U’ L) (U2 R U2 R') | Better for one-handed solves |